The present study showed that the marching cube algorithm for soft tissue landmark detection had high intra- and inter-examiner reliability. Moreover, a newly proposed coordinate, the CC point, was more consistent than manual digitation, and was thus validated as a more consistent and reliable landmark in clinical practice.
The marching cube algorithm was used in Program S to reconstruct the soft tissue data and form contour lines and tabletops to facilitate the digitization of the soft landmarks. The principle for the formation of contour lines via the marching cube algorithm is as follows. In 2D space, the marching cube algorithm divides the space into uniform cell units and divides the cells in and out of the circle (Fig. 7A). Boundaries can quickly be drawn while matching the dictionaries of the 16 possible cases (Fig. 7B). Subsequently, the distance from the center to the edge was approximated as the actual distance (Fig. 7C). All 16 2D marching cubes combinations are used to make the boundaries (Fig. 7D). In 3D space, this algorithm uses a cube as a unit to form an isosurface. The cube configurations formed during the triangulation step can generally be categorized into 15 unique patterns identified in the original marching cube algorithm (Fig. 7E)20. Therefore, the marching cube algorithm independently selects 1 of 15 patterns in each cell, enabling parallel processing, and then processes single-image results on a unique surface.
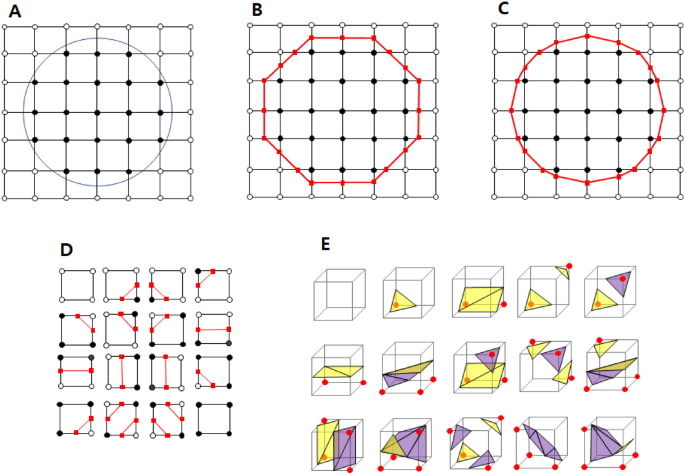
Marching cube algorithm. (A) The algorithm divides the space into uniform cell units and divides the cells in and out of the circle. (B) Boundary making matching the dictionary of 16 possible cases. (C) Distance from the center to the edge is approximated to the actual distance. (D) All 16 2D marching cube combinations used to make the boundary. (E) All 15 3D marching cube combinations used to make the boundary.
The degree of smoothing of the contours made by the marching cube algorithm is affected by the resolution of the 3D image: the higher the resolution, the smaller the size of the cube making up the surface, and as a result, more detailed surface images and dense contours can be obtained. Therefore, a smooth surface in which contours are not clearly visible is obtained after surface reconstruction using a marching cube algorithm, such as an intraoral scanner, for equipment with high spatial resolution. The CBCT images used in this experiment had a spatial resolution of 0.3 mm with an FOV of 16 × 16 cm, and this relatively low spatial resolution caused stepped contours and mountain tabletop effects to be generated during reconstruction with the marching cube algorithm. The result of these different resolutions is clearly visible in the marching cube results of the CBCT images with different resolutions.
Therefore, by this process, Program S showed a slight difference in the height of the soft tissue as a contour line and served as a guide when digitizing landmarks manually. Digitizing 3D soft tissue landmarks via contour lines reduces errors when evaluating 3D structures via 2D screens and resolves issues with soft tissue appearing differently when the rendered images are rotated or when the contrast, opacity, or brightness are manipulated. As a result, the intra- and interclass correlation coefficients were close to 1, indicating that the exact same point could be measured multiple times. Moreover, the difference in the measurement values between examiners (Δx, Δy, Δz, Δd) for Program S was less than that for Program A, and the differences were close to zero. In other words, the precision of the landmarks between examiners was higher when using Program S compared to Program A. Furthermore, in the present study, by calculating the average coordinates of the points on the tabletop, the CC point of the 3D soft tissue was obtained. There was no difference in the landmarks depending on the acquisition time and examiners, and it was possible to obtain completely consistent measurements. That is, it was possible to digitize the 3D soft tissue landmarks more reliably and objectively using Program S and CC points (especially cheek points on both sides). Since orthodontic and surgical treatments are mostly irreversible, treatment plans should be established not just by instinct, but with accuracy. In this study, we proposed a methodology for digitizing soft tissue landmarks that is highly reliable; therefore, by using this methodology, more accurate research can be conducted regarding soft tissue changes before and after treatment.
Using Program S, detailed digitization was possible even on other soft tissue areas and not on specific landmark points. For example, in Sample 23, two high contour lines were observed on the lower lip (Fig. 3). This meant that the patient’s lips were slightly concave in the center. In Program A, it was difficult to observe these characteristics. Therefore, Program S can be used for delicate soft tissue changes caused by soft tissue fillers or botulinum toxin.
Various methods, such as 3D-stereophotogrammetry19,21, Moire topography22, optical surface scans23, laser scanning24,25, and CBCT scans6,9,19, have been introduced to acquire 3D facial soft tissue data. In this study, CBCT was used for soft tissue data acquisition because the subjects underwent CBCT taking for the extraction of wisdom teeth. Likewise, orthodontists and oral-maxillofacial surgeons mostly modify the hard tissues (skeletal and teeth) to acquire the desired soft tissue change. Therefore, CBCT is the most convenient choice for acquiring both hard and soft tissue data simultaneously. Moreover, a previous study showed that CBCT is the most efficient and reliable imaging tool for soft tissues26, and so using CBCT for soft tissue evaluation was a reasonable choice for this study. However, CBCT inevitably exposes patients to radiation27. Therefore, in the cosmetic field, the degree of skin shrinkage or skin elasticity is often evaluated using 3D-stereophotogrammetry21 and Moire topography methods22, limiting radiation exposure. If the clinician uses only soft tissue procedures, such as botulinum toxin or fillers, laser scanners are often used as a simple method24,28. Previous studies defined soft tissue landmarks based on the underlying hard tissue structures; consequently, if there is no hard tissue data, clinicians cannot detect soft tissue landmarks29. Moreover, soft tissue landmarks determined based on the underlying hard tissue are not always clinically meaningful, since as the soft tissue elasticity decreases or as the patients become more obese, the soft tissue becomes less associated with the underlying hard tissues30,31,32. This study provides a reliable method for digitizing soft tissue landmarks without the need for hard tissue. Therefore, this method can be applied to soft tissue acquisition methods other than CBCT. Further research on applying this method to other soft tissue acquisition methods will be conducted in the future, but similar results are expected as the marching cube algorithm can be applied to any data.
Until now, comparisons before and after treatment were inaccurate because there was a lack of studies that questioned the reliability of the current method of digitizing soft tissue landmarks. Therefore, most studies used 3D facial heatmaps to show changes in the soft tissue profile33. Using only heatmaps, clinicians are unable to determine the exact amount of soft tissue changes, leading to inaccurate treatment plans. Compared to heatmaps, digitizing landmarks and evaluating the change in these landmarks before and after treatment would allow clinicians to determine the exact changes.
In previous studies, most soft tissue landmarks were digitized on the lower facial area and along the midsagittal plane6,7,8. However, Ferrario et al.35 in actual clinical practice, meaningful soft tissue landmarks are not necessarily located along the midsagittal plane. In particular, there are not enough standards and evaluations on features of the cheek area, which occupies a large portion of the face. Soft tissue of the cheek area relies on the structure of the underlying hard tissue to a certain extent; however, features such as protrusion and inversion of the cheeks vary depending on muscle development, amount of subcutaneous fat, patients’ sex, age, and elasticity of the skin tissue6. As a result, the definition and method of measuring landmarks on the cheek area differed amongst each study. According to Menezes et al., it was defined as the intersection of Camper’s plane and a line connecting the external eye canthus with the labial commissure34,35. In another study, it was defined as the intersection of the vertical line passing through the mid-canthus parallel to the z-axis and the horizontal line passing through the ala and perpendicular to the vertical line36. This area did not protrude from the center of the cheek, nor was it in the middle of the cheek area; neither point was clinically meaningful. Hence, before-and-after evaluations of cheek area modifications such as MEDPOR augmentation37, soft tissue treatments with botulinum toxins38,39,40, malar-plastic surgery41, and changes in soft tissue when treated by mini-screw-assisted rapid palatal expanders36 could not be precisely assessed using these landmarks. However, in this study, when using the marching cube algorithm to digitize dots on the cheeks (Ch_r, Ch_l) using Program S, the most protruding area could be evaluated, which is clinically significant, and can possibly be applied to the evaluation of the forementioned treatments.
The developed algorithm can be applied not only to the field of medical imaging, but also to various studies that require reference points on various curved surfaces, such as animation, 3D land or remains surveys, and nanosurface measurements. The marching cube algorithm produces a mesh that is a rough approximation of the true isosurface and is not well suited to sharp corners or creases42. However, the developed algorithm was implemented on a soft, relatively simple face-shaped image with low enough resolution to show the mountain tabletops and contour lines, which is an acceptable use of the marching cube algorithm. Since mountain tabletops, which are the result of the marching cube algorithm, are objects that can be easily recognized visually, it is expected that the entire process can be fully automated through automatic segmentation using deep learning in the future.
There are a few limitations of this study. First, due to the scattered radiation, soft tissue data acquired via CBCT have low contrast resolution43. Despite the convenience of CBCT, applying any algorithm to reconstruct the CBCT soft tissue data has risks of analyzing inaccurate data. However, previous studies indicated that there were no clinical differences between other types of soft tissue acquisition methods11,44; therefore, the results of this study could be considered acceptable. Nevertheless, future studies are needed to determine whether similar results are obtained for other acquisition methods. Second, only six landmarks were included in this study. More landmarks could have been included, such as soft tissue pogonion or glabella. However, in the process of immobilizing the patient during CBCT acquisition, deformation of the soft tissue pogonion and glabella was caused by the chin and forehead resting on the CBCT scanner. Therefore, based on the results of this study, future studies using CBCT data without deformation of the chin and forehead are required. In the case of soft tissue gonions, manual digitation by using Program S was also possible for most subjects. However, the soft tissue gonion was difficult to detect in subjects that lacked soft tissue elasticity. Moreover, because of the overlapping contour lines in the gonion area, it was difficult to develop the CC point using the current algorithm. Finally, only convex landmarks were evaluated in this study. Contour lines made by the marching cube algorithm made stable tabletops on convex points but not on concave points. An improved algorithm and methodology should be developed to overcome these limitations.

