DeNTNet: Deep Neural Transfer Network for the detection of periodontal bone loss using panoramic dental radiographs

This study was approved by the institutional review board of Korea University Anam Hospital(IRB No.2016AN0267) with a waiver of informed consent. The dataset collection and experiments were performed in accordance with the approved ethical guidelines and regulations.

Data collection and annotation

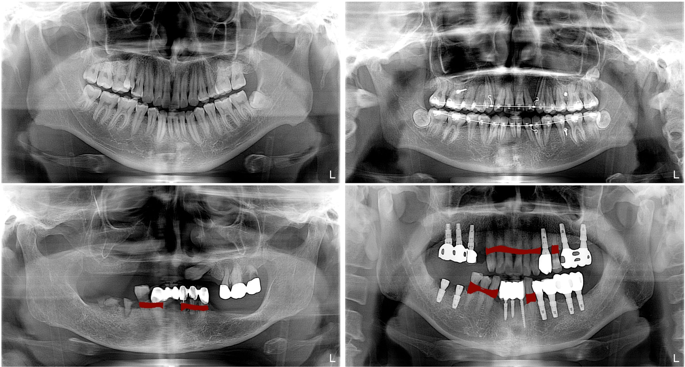
A total of 12,179 panoramic dental radiographs were retrospectively collected from Korea University of Anam Hospital after removing identifiable patient information during the period between ({1}^{{rm{st}}}) Jan. 2014 and (1{4}^{{rm{th}}}) Feb. 2016. The radiographs were taken with devices from multiple vendors: DENTRI (HDXWILL, South Korea), Hyper-XCM (Asahi, Japan), CS 9300 (Carestream Dental, USA), Papaya (Genoray, South Korea), and PHT-30LFO (Vatech, South Korea). Only one radiograph per patient is included by excluding all follow-up exams taken during data collection, and the patients’ gender and age distribution is described in the appendix. Since the intra and inter-examiner agreement of PBL is considered to be low^4,11, five dental clinicians who are experienced dental hygienists with 5, 9, 16, 17, 19 years of practice for assessing dental radiographs independently masked the PBL lesions and recorded the corresponding tooth number for annotation. During the course of data collection, the annotation quality was continuously monitored by a separate dental expert who has been in clinical dental practice for over 15 years as a board-certified oral and maxillofacial surgeon. For teeth numbering, the Federation Dentaire Internationale (FDI) teeth numbering system (ISO-3950) was used¹² and there are 32 teeth in total, as shown in Fig. 2. To construct the reference dataset, the five teeth-level annotations were aggregated using the following rule:

where (i) is the data index ((N=12,179)), (j) is the tooth index ((T=32)), and (l) is the annotator index ((L=5)). Here we set ({C}_{R}=3) which corresponds to majority voting. We randomly split the dataset into training (({N}_{tr}=11,198)), validation (({N}_{val}=190)), and test (({N}_{tst}=800)) sets.

Overall framework

The overall framework of the proposed method consists of multiple stages, as illustrated in Fig. 2. At the first stage, we trained a region of interest (ROI) segmentation network to extract the teeth related region. In the next stage, a lesion segmentation network was trained to predict the PBL lesions. By exploiting the encoder part of this lesion segmentation network as a pre-trained model, we trained a classification network that predicts the existence of PBL in each tooth. To further improve performance, we also train a separate classification network, that predicts the existence of PBL lesions specifically for the premolar and molar teeth types. The two classification networks are ensembled to make the final PBL lesion prediction. The detailed procedures are described in the following sections, and the contribution of each stage to the final PBL detection performance is also analyzed in the ablation study.

Region of interest segmentation

As can be seen in Fig. 1, there is a wide variability in the field of view and contextual information in the panoramic dental radiographs, depending on the patients and devices. This variability impedes the detection of PBL lesions, which are only relevant in the teeth regions in the radiograph. To accommodate this variability, we trained a segmentation network which automatically extracts the ROI. The ROI segmentation model ({f}^{R}) has an U-shaped architecture employed by Ronneberger et al.⁵ which consist of an encoder part ({f}_{E}^{R}) and a decoder part ({f}_{D}^{R}). The detailed architecture of our ROI segmentation model can be found in the appendix.

To train and validate the ROI segmentation network, we randomly selected 440 panoramic dental radiographs from the entire training dataset ((N)=11,189). The ROI segmentation network was trained using 400 randomly sampled radiographs until its performance validated on the remaining 40 radiographs converged. The ROIs were annotated as binary polygon masks by an experienced dental clinician, starting from the right temporomandibular joint (TMJ) connected in order of the right mandible, left mandible, and left TMJ as shown in Fig. 2(a). The radiographs and their corresponding masks were resized to resolution (512times 1024).

We used binary cross-entropy with ({L}_{2}) regularization defined below as the loss function ({L}_{R}) for the ROI segmentation network

where (n) denotes the number of pixels in the radiograph indexed by (i), ({y}_{i}^{R}) is the binary label for pixel (i), ({hat{y}}_{i}^{R}) is the predicted label for pixel (i), and (lambda ) is a regularization parameter which we set to (1{0}^{-4}). The ROI segmentation network was trained for 50 epochs using the Adam optimizer¹³ and the initial learning rate was set to (1{0}^{-4}) obtained from hyperparameter tuning.

After training, the predicted ROI masks were post-processed with a morphology operation filling the holes in the segmented mask using binary_fill_hole function in the SciPy package¹⁴. The convex hull of the resulting masks was computed using the OpenCV¹⁵convexHull function and the regions in the corresponding bounding box were extracted and resized to (512times 1024). Finally, the extracted image excluding the black background area outside of the predicted mask in the radiograph was normalized using (z)-score. The validation dice coefficient increased from 0.95 to 0.98 after post-processing.

Pre-training for transfer learning

While the goal of the proposed framework is to provide tooth level prediction, there are a limited number of positive PBL examples for each tooth(the number can be found in the appendix). This lack of data and class imbalance is even more severe for the molar teeth, which is problematic for training deep neural networks, where an abundant training dataset is necessary to learn complex and diverse patterns such as PBL in radiographs. We work around this issue by employing transfer learning, which utilizes the learned weight from one task as the initial weight of a new network, which is then trained for a different task. Transfer learning is especially useful in medical image analysis and has been widely adopted in this domain because acquiring annotated medical data is expensive and time-consuming⁷.

We trained a lesion segmentation network ({f}^{S}) with the same U-shape architecture as the ROI segmentation network, which learns to extract salient features of PBL as shown in Fig. 2(b). The PBL lesion segmentation model has the same network architecture as the ROI segmentation network ({f}^{R}) but has a different loss function. Specifically, focal loss was used to address the imbalance between positive and negative samples in the pixel level¹⁶:

where (n) is the number of pixels indexed by (i) in the ROI-extracted radiograph and (gamma ) denotes the focal loss parameter, which was set as 2 in our study. Here the PBL lesion segmentation masks provided by five dental clinicians were aggregated using the following rule:

where (i) is the index of the pixel in the ROI-extracted radiograph and (l) is the index of annotator ((L=5)). In order to enhance recall rate and facilitate learning various features of PBL, we set ({C}_{S}=1) which means ({y}_{i}^{S}) is the union of masks annotated by the five dental clinicians. The lesion segmentation network was trained for 50 epochs using Adam optimizer, and the initial learning rate was set to (1{0}^{-5}) obtained by hyperparameter tuning. The entire training dataset ((N) = 11,189) was used to train the lesion segmentation network until its performance on the validation dataset ((N=190) was maximized. Data augmentation was performed using random rotation (le ,10) degrees, horizontal and vertical shift (le 10 % ), and shift of brightness, sharpness, contrast (le 15 % ).

Tooth-level PBL classification

In clinical dental practice, it is mandatory to report the dental disease along with the teeth numbers of the lesions. However, providing lesion segmentation masks requires additional effort to assign teeth numbers to the corresponding lesion, which is subjective and time-consuming. Therefore, to make the computer-assisted diagnostic support system more clinically applicable in dental practice, it is desirable to provide teeth number for the detected lesions. Therefore, we formulated the PBL detection problem as a multi-label classification task where the existence or absence of PBL is predicted simultaneously for each tooth.

As mentioned in the previous section, training this multi-label network directly from tooth-level annotations with randomly initialized weights requires a plethora of training examples for each tooth to learn diverse and complex representation of PBL lesions. To deal with the scarcity of positive training examples in the tooth-level annotations, we transferred the weights from the encoder part ({f}_{E}^{S}) of the lesion segmentation network ({f}^{S}) to the multi-label classification network ({f}^{A}) as pre-trained weights. Two additional convolution blocks, one global average pooling layer, and two fully connected layers are attached to the end of the encoder ({f}_{E}^{A}). Finally, the output layer consists of 32 nodes, which correspond to the binary classification output for each tooth. The detailed architecture of the tooth-level classification model can be found in the appendix. All the layers, including the encoder part initialized with the transferred weights from the lesion segmentation network, were trained for the tooth-level classification task.

Another difficulty which arises in PBL classification is that premolar and molar teeth represent a more complex morphological structure, which hinders the detection of PBL in the panoramic dental radiographs. To overcome this difficulty, another tooth-level classification network ({f}^{B}) was trained specifically for the premolar and molar teeth. While ({f}^{A}) and ({f}^{B}) share the same network architecture, ({f}^{B}) was trained with a vertical split of the ROI image as the input, generated by ({f}^{R}), and the label-masked multi-label as the output as shown in Fig. 2(d). Here the label-masks were applied to incisors and canines by assigning zero to the corresponding labels; therefore, ({f}^{B}) takes as input an ROI image and is trained to predict PBL in only premolar and molar teeth. The transferred weight from ({f}_{E}^{S}) was also used to initialize ({f}^{B}). To train the teeth-level classification model ({f}^{C}={,{f}^{A},{f}^{B}}), focal loss with ({L}_{2}) regularization is used for each output node computed as:

where (N) is the number of training examples indexed by (i), (j) is the corresponding tooth index, (k) is the trainable weight index, and (gamma ) denotes the focal loss parameter, which was set to 2. We applied the same data augmentation technique as in the pre-training for transfer learning section above. Both ({f}^{A}) and ({f}^{B}) were jointly trained using the entire training dataset ((N)=11,189) until their performance on the validation dataset ((N)=190) converged. Because ({f}^{B}) takes the vertical split of ROI images as illustrated in Fig. 2, the effective number of training samples for ({f}^{b}) is twice ((N=22,378)) the number of the training dataset. As stated in Equation 4, the majority vote of the annotators for each tooth was used as target labels to train the model.

At the inference phase, we aggregated the prediction of ({f}^{A}) and ({f}^{B}) as follows:

where (j) is the tooth type index and ({In},{Ca},{Pr},{Mo}) denotes the index set of incisor, canine, premolar, and molar teeth, respectively. ({x}_{{rm{ROI}}}) is a ROI image with resolution (512times 1024) given by the output of ({f}^{R}) and ({x}_{{rm{ROI}}/2}) is its vertical split image with resolution (512times 512). (alpha ) is a hyperparameter which was set to (0.1) in our study attained by hyperparameter tuning.

Auxiliary co-occurrence loss

While the encoder part of the tooth-level classifier is shared to extract salient features for PBL detection, the predictions for each tooth at the output layer are made independently without considering the clinical knowledge that PBL lesions frequently co-occur across horizontally adjacent teeth. As shown in Fig. 3, there is a high co-occurrence of PBL among incisors and canines, while the co-occurrence among premolar and molar teeth is lower in both maxillary (upper jaw) and mandibular (lower jaw) teeth. Also, the third molar had noticeably low co-occurrence of PBL with other teeth except the third molar at the opposite side.

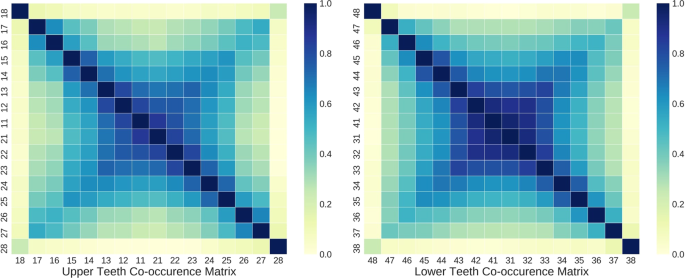
Co-occurrence matrix among teeth with PBL in the training dataset. (Left) Correlation matrix among maxillary (upper jaw) teeth, (Right) Co-occurrence matrix among mandibular (lower jaw) teeth.

To exploit this prior information for improving the generalization performance of PBL detection, auxiliary co-occurrence loss is computed as:

where both (j) and ({j}^{^{prime} }) are the tooth index, ({y}_{j}) is the binary label derived from Eq. (4), ({hat{y}}_{j}) is the network output, and ({C}_{j{j}^{^{prime} }}) is the element of the co-occurrence matrix (Cin {{mathbb{R}}}^{ktimes k}), and (k(=16)) is the number of teeth in the upper or lower teeth. (Z={max }_{j},{c}_{j}) is the normalization term which guarantees all ({c}_{j})’s lie between 0 and 1.

The auxiliary co-occurrence loss was applied separately for upper and lower teeth based on their respective co-occurrence matrix, and the final loss function ({L}_{F}) used to train the tooth-level classification network is defined as

where ({L}_{C}) is focal loss defined in Eq. 5, (beta ) is a hyperparameter set to (0.01), and ({1}_{{jin U}}) and ({1}_{{jin L}}) correspond to the indicator function for the upper and lower teeth, respectively. We trained the tooth-level classification network for (100) epochs using Adam optimizer and the initial learning rate was set to (1{0}^{-5}) which was obtained by hyperparameter tuning.